I barely remember when the last time I implemented the famous Fibonacci was. It was the doctrine example of recursive implementation. I am not sure whether it is still a thing at the moment.

Over the weekend, I read some recent stuff in C#. The Fibonacci came to my mind. I have not tried to implement it differently and have not tested how bad it is with recursive implementation. So it is fun to have write some code.

Given that we need to know the result of F30 (or F40), how long would it take and how many calls in the recursive approach? And how about the alternative implementation?

Recursive Implementation

class Program
{
    private static int _recursiveCount = 0;
    private static long RecursiveFibonacci(int n)
    {
        _recursiveCount++;
        return n < 2 ? n : RecursiveFibonacci(n - 1) + RecursiveFibonacci(n - 2);
    }

    private static void DisplayFibonacci(Func<int, long> fibo, int number)
    {
        Console.WriteLine($"{number}: {fibo(number)}");
    }

    static void Main(string[] args)
    {
        const int number = 30;
        var stopwatch = new Stopwatch();
        stopwatch.Start();
        DisplayFibonacci(RecursiveFibonacci, number);
        stopwatch.Stop();

        Console.WriteLine($"Completed after: {stopwatch.Elapsed}; Recursive Counts: {_recursiveCount}");
    }
}

Run and observe the result

Completed after: 00:00:00.0457925; Recursive Counts: 2.692.537

The completion time depends on the computer the code runs. But the recursive count is impressive—2.5 millions time. I increased the number to 50 but lost my patient to wait.

Recursive with Cache

We could improve the recursive solution with result caching. Again, this is a simple implementation for fun.

private static readonly List<long> _fiboCache = new List<long> { 0, 1 };
private static long FibonacciRecursiveWithCache(int n)
{
    _recursiveCount++;
    while (_fiboCache.Count <= n)
    {
        _fiboCache.Add(-1);
    }

    if (_fiboCache[n] < 0)
    {
        _fiboCache[n] = n < 2 ? n : FibonacciRecursiveWithCache(n - 1) + FibonacciRecursiveWithCache(n - 2);
    }

    return _fiboCache[n];
}

For Loop Implementation

And I gave a try with non-recursive approach. There are more lines of code but runs so much faster

private static long FibonacciForLoop(int n)
{
    long n_1 = 1;
    long n_2 = 1;
    long total = 0;
    for (int i = 3; i <= n; i++)
    {
        total = n_1 + n_2;
        n_1 = n_2;
        n_2 = total;
    }

    return total;
}

I do not need 3 variables (n_1, n_2, total). The solution only needs 2 variables. However, I felt natural with 3 variables. It follows the way I calculate it manually.

So let put them together and see the differences

static void Main(string[] args)
{
    const int number = 30;

    Console.WriteLine("Recursive");
    var stopwatch = new Stopwatch();
    stopwatch.Start();
    DisplayFibonacci(RecursiveFibonacci, number);
    stopwatch.Stop();

    Console.WriteLine($"Completed after: {stopwatch.Elapsed}; Recursive Counts: {_recursiveCount}");

    Console.WriteLine("Recursive with cache");
    _recursiveCount = 0;
    stopwatch.Reset();
    stopwatch.Start();
    DisplayFibonacci(FibonacciRecursiveWithCache, number);
    stopwatch.Stop();

    Console.WriteLine($"Completed after: {stopwatch.Elapsed}; Recursive Counts: {_recursiveCount}");

    Console.WriteLine("For loop");
    stopwatch.Reset();
    stopwatch.Start();
    DisplayFibonacci(FibonacciForLoop, number);
    stopwatch.Stop();

    Console.WriteLine($"Completed after: {stopwatch.Elapsed}");
}

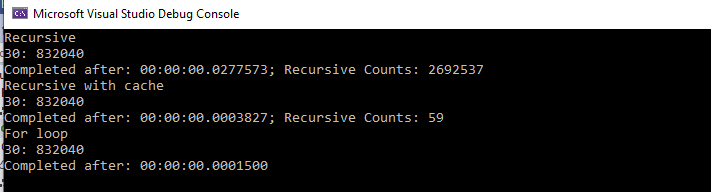
Ladies and gentlemen, I present to you

Recursive
30: 832040
Completed after: 00:00:00.0277573; Recursive Counts: 2692537
Recursive with cache
30: 832040
Completed after: 00:00:00.0003827; Recursive Counts: 59
For loop
30: 832040
Completed after: 00:00:00.0001500

That’s it! I know how to implement the Fibonacci.